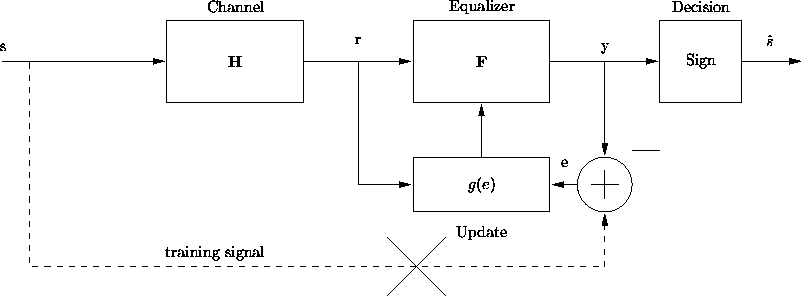
Figure 3.4: Direct Adaptive Blind Equalization

A natural question from for direct adaptive equalization with
training is, ``How can we adapt our filter, ![]() , without
the use of a training signal?''. Figure 3.4 shows such a
system. There has been extensive research
on this subject for single user applications as well as multi-user
applications. The Constant Modulus Algorithm is one such algorithm
employed for the blind adaptation problem. This algorithm is of the
gradient decent type that minimizes the following cost function.
, without
the use of a training signal?''. Figure 3.4 shows such a
system. There has been extensive research
on this subject for single user applications as well as multi-user
applications. The Constant Modulus Algorithm is one such algorithm
employed for the blind adaptation problem. This algorithm is of the
gradient decent type that minimizes the following cost function.
![]()
where ![]() is defined as the kurtosis of
the source and y is the soft decision output of
is defined as the kurtosis of
the source and y is the soft decision output of ![]() . Note that
. Note that
![]() for a BPSK source, hence the constant modulus terminology. It
has been shown to be robust to channel under modeling and adaptive
channel noise as well as exhibiting other desirable
properties. [7] The update equation for CMA can be written
in a similar fashion as the LMS algorithm.
for a BPSK source, hence the constant modulus terminology. It
has been shown to be robust to channel under modeling and adaptive
channel noise as well as exhibiting other desirable
properties. [7] The update equation for CMA can be written
in a similar fashion as the LMS algorithm.
![]()
where the ![]() in the LMS algorithm has been replaced with
in the LMS algorithm has been replaced with
![]() . One of the properties of the CMA cost function
is that it is multi-modal, meaning there is more than one achievable
minimum. In a single user case these minima correspond to different
delays and different polarities. In certain cases of noise and
channel characteristics, the depth of these minima can vary
greatly. It turns out that initialization of this
algorithm directly effects which minimum will be achieved. One
recent reference addressing CMA regions of convergence is [8].
. One of the properties of the CMA cost function
is that it is multi-modal, meaning there is more than one achievable
minimum. In a single user case these minima correspond to different
delays and different polarities. In certain cases of noise and
channel characteristics, the depth of these minima can vary
greatly. It turns out that initialization of this
algorithm directly effects which minimum will be achieved. One
recent reference addressing CMA regions of convergence is [8].
The problem of initialization becomes an even more complex issue when we
consider the multiuser case. The received signal at the demodulator
in a DS-CDMA system is a sum of K BPSK valued sequences (assuming BPSK for
simplified case) spread by each user's spreading code and affected
by channel ISI (i.e. ![]() as in chapter 2).
Essentially, this corresponds to K different
sets of CMA minima where a set consists of one users minima.
Now there are K
times as many minima to converge to when employing the Constant
Modulus Algorithm for DS-CDMA. The problem of initialization
becomes even more important in the multiuser case. Now we could not
only converge to an undesirable minima; we could actually converge to
a minima of the wrong user. Schniter has proposed a method of
initialization of CMA for DS-CDMA in [9] that will be briefly
described below.
as in chapter 2).
Essentially, this corresponds to K different
sets of CMA minima where a set consists of one users minima.
Now there are K
times as many minima to converge to when employing the Constant
Modulus Algorithm for DS-CDMA. The problem of initialization
becomes even more important in the multiuser case. Now we could not
only converge to an undesirable minima; we could actually converge to
a minima of the wrong user. Schniter has proposed a method of
initialization of CMA for DS-CDMA in [9] that will be briefly
described below.
The proposed scheme would test the outputs of a bank of time shifted
matched filter hypotheses of the desired user and initialize the CMA
algorithm with the hypothesis corresponding to the output with the
minimum kurtosis. The reason for choosing the initialization based on
the minimum kurtosis is as follows. If we assume the desired user is chip
synchronized, then the output of the hypothesized initialization corresponding to the
desired users delay is going to consist of two parts. One will be the
actual source symbols sent by the desired user, and the other portion
will be the Multiple Access Interference assuming no channel ISI. (see
section 3.1.1 on matched filter)
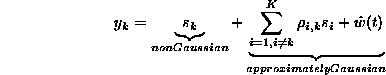
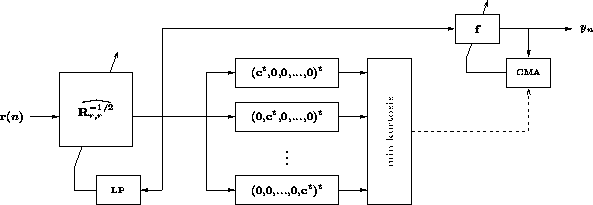
This method seems quite appropriate for initializing CMA, however, we must
consider non-equal power users. The near-far problem has
effects on the CMA minima and regions of convergence. Weak users will
have small regions of convergence which increases the risk of
misconvergence. Since the regions of convergence are proportional to
the eigenvalues of the received data autocorrelation matrix, a
pre-whitening technique is proposed. By pre-whitening the received
data, the near-far effect is minimized and the probability of
convergence is increased dramatically. A block diagram of the
proposed scheme for initializing CMA is shown in figure
3.5.![]() In the block diagram,
In the block diagram, ![]() refers to the autocorrelation matrix of the received data.
refers to the autocorrelation matrix of the received data.