Conventional Detector (Matched Filter)

 

  
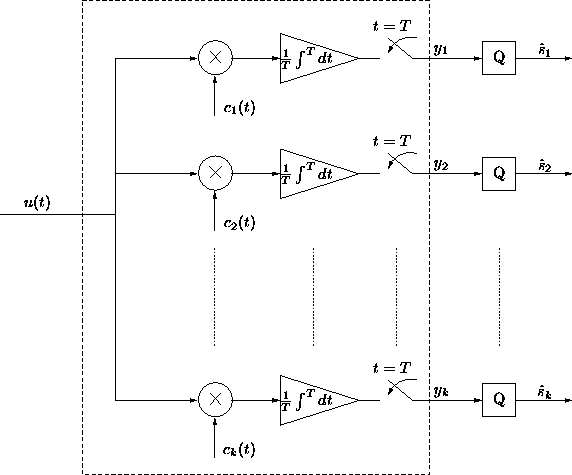
Figure 3.1: Conventional DS-CDMA Detector.

The conventional detector, also known as the matched filter detector, simply correlates the received signal with the desired user's time reversed spreading waveform, and samples the output at the bit rate. This method of detection comes straight from single user designs. It does not take into account any other users in the system or channel dynamics and therefore is not robust to asynchronism, fading channels, or pn sequences with substantial cross correlation. A model of the conventional detector is shown in figure 3.1. Note that the chip matched pulse shaping filter is not shown separately, because the pulse-shape is included in . Assuming a bit synchronous system with no channel dynamics or power variations, the output of the conventional detector is defined as

where is the cross correlation defined by

and is the filtered AWGN. This ensures for normalized spreading codes that when i=k, , and when , . This emphasizes the need for low cross-correlation between the spreading codes, otherwise the MAI term will dominate the correlator output. The MAI also increases with the number of users active in the system and is very susceptible to power variation among users. A strong interfering user will cause the MAI to increase, overpowering the desired user. Multiple Access Interference can cause high bit error rates and poor ultimately decrease system capacity.

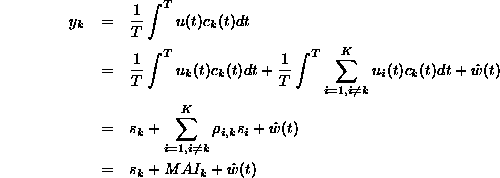
This near-far problem can be overcome by using power control, but this necessitates an increase in complexity at both the receiver and the transmitter. Power control can be implemented in two different ways. The mobile unit can detect the power of the received base station signal and transmit at the inverse of the power. The other option is for the base station to transmit instructions to the mobile units. Another way of reducing MAI is the use of sectored antennas. These antenna can focus on a certain area of coverage, eliminating affects of users in different sectors. In the IS-95 system, detectors matching the random spreading code are used to receive the data. In order to overcome the MAI and the near-far effect, a combination of source coding and power control is used.

So we can conclude that the matched filter detector will perform optimally in a synchronous system with no channel ISI, orthogonal spreading codes, equal power users, and no neighboring cell interference. The desirable property of the matched filter is its very low computational complexity. The question really is, ``How poorly will it perform when these conditions are not met?'' We can use the simulation tools, as done in section 5, to make some observations which will help us answer this question.