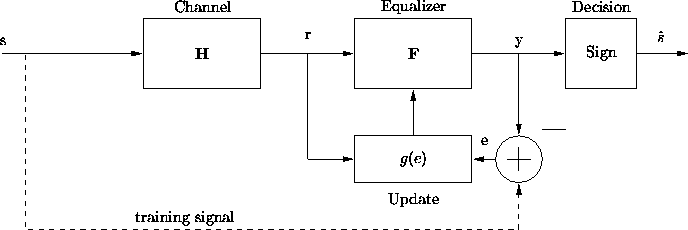
Figure 3.3: Direct Adaptive Equalization

Direct adaptive receivers with training signals employ structures
like the one shown in figure 3.3. The idea is to send a
training signal, s, which can be used to update the equalizer coefficients
using a chosen algorithm. An error term e is calculated from the
difference between the training signal and the soft decision output,
y. Then an algorithm implementing the function g(e) is used to
update the filter coefficients. Two popular algorithms for this type of
implementation are the Least Mean Squares (LMS) and the Recursive
Least Squares (RLS) algorithms. The RLS algorithm converges faster
than the LMS algorithm, but is more computationally expensive. There are
methods of implementing the RLS algorithm with reduced complexity, but
they were not considered in this project.![]()
The LMS algorithm readily lends itself to the developed system
model. In a DS-CDMA system, the training signal would consist of
symbols known to the intended receiver. The interesting property LMS
imparts to the DS-CDMA system is the lack of a need for the intended
user's spreading sequence or any of the other user's spreading
sequences. All of the fixed receivers assumed
knowledge of the spreading codes associated with each user. If we
implement a receiver using LMS, all that is needed is knowledge of a
finite length training sequence ![]() . This also implies that the equalizer
will only be updated at the symbol rate, not the chip rate.
The update equation for LMS is as follows,
. This also implies that the equalizer
will only be updated at the symbol rate, not the chip rate.
The update equation for LMS is as follows,
![]()
Where ![]() is the length
is the length ![]() regressor vector as defined in
chapter 2,
regressor vector as defined in
chapter 2, ![]() is the chosen positive update step size, and
is the chosen positive update step size, and
![]() . Since the regressor is arriving at the chip rate and
our updates are only occurring at the symbol rate, it is important to
note the relationship of
. Since the regressor is arriving at the chip rate and
our updates are only occurring at the symbol rate, it is important to
note the relationship of ![]() and
and ![]() . If
. If
![]() then
then ![]() where L is the spreading gain and P is
the oversampling factor.
where L is the spreading gain and P is
the oversampling factor.
The LMS implementation of a DS-CDMA receiver may prove to be a viable option in certain scenarios where the channel does not change rapidly. It is a useful algorithm because it does not require knowledge of the spreading sequences, user powers, or channel estimates. However, the convergence speed is relatively low, and bandwidth will be consumed for the training sequence. In order to do without a training sequence we will have to look at blind adaptive algorithms