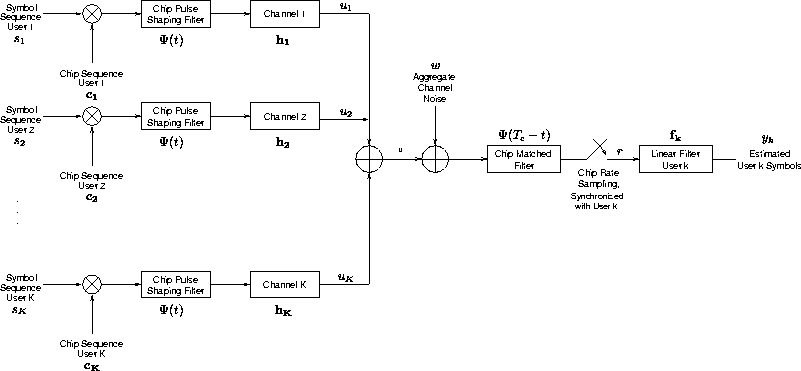
Figure 2.1: DS-CDMA system model.
Due to the complex nature of CDMA systems, there have been many different formulations for the CDMA model. The model presented here is designed to have a form which is convenient for linear detection formulation. It can also be found in [3, 1]

Consider the DS-CDMA baseband system model shown in Figure 2.1.
In this model we have K users transmitting symbols
from the BPSK alphabet ![]() with arbitrary power and timing.
Each user's symbol is spread by an
arbitrary periodic pseudo-noise sequence of length L. The symbol period
is denoted by T and the chip period is denoted by
with arbitrary power and timing.
Each user's symbol is spread by an
arbitrary periodic pseudo-noise sequence of length L. The symbol period
is denoted by T and the chip period is denoted by ![]() where
where ![]() .
All users are assumed to use
the same chip pulse shaping filter, denoted by
.
All users are assumed to use
the same chip pulse shaping filter, denoted by ![]() which is
assumed to be time limited to
which is
assumed to be time limited to ![]() .
All channels (including any attenuation
in the kth user's transmission path) are assumed FIR, denoted by
h(t), with maximum delay spread
.
All channels (including any attenuation
in the kth user's transmission path) are assumed FIR, denoted by
h(t), with maximum delay spread ![]() (
(![]() a positive integer).
The aggregate channel noise is denoted by
w(t) and is assumed Gaussian, zero mean, and independent of the sources, with
variance
a positive integer).
The aggregate channel noise is denoted by
w(t) and is assumed Gaussian, zero mean, and independent of the sources, with
variance ![]() . The chip matched
filter is the usual
. The chip matched
filter is the usual ![]() , see [4].
Unless noted otherwise, the following notation applies to the rest of this
paper. Baud spaced indexes are represented by n. Chip spaced indexes
are represented by l.
User k's nth symbol is denoted by
, see [4].
Unless noted otherwise, the following notation applies to the rest of this
paper. Baud spaced indexes are represented by n. Chip spaced indexes
are represented by l.
User k's nth symbol is denoted by ![]() .
User k's spreading sequence is denoted by
.
User k's spreading sequence is denoted by
![]() where
where
![]() .
Soft decisions
at the output of the linear estimator are denoted by
.
Soft decisions
at the output of the linear estimator are denoted by ![]() where
where ![]() is the composite system delay in units of T.
is the composite system delay in units of T.
With all of this out of the way, we can write the following general expressions
to develop a continuous time model. First, let us express the kth user's
continuous time spreading waveform as
![]()
then the output of the kth channel may be written as
We now wish to sample the received signal u(t) after pulse-matched
filtering and apply a FIR linear filter ![]() . The FIR linear
filter used to estimate symbols from the kth user is denoted by the
length
. The FIR linear
filter used to estimate symbols from the kth user is denoted by the
length ![]() vector
vector ![]() .
.
Now, let us consider some special cases. In each case, we will first work
to reduce the continuous time description to an equivalent discrete time
model. The discrete time model will then be used to calculate MMSE
optimal settings for ![]() , including adaptive solutions.
, including adaptive solutions.