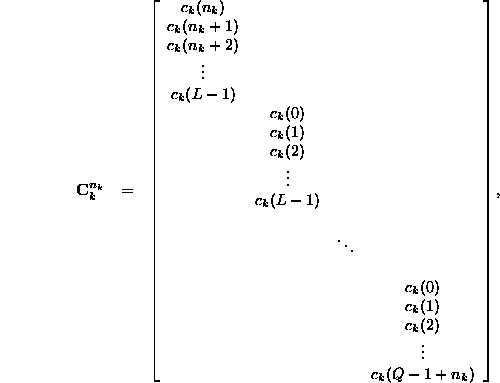It is essential to be able to develop a finite discrete time model of the
asynchronous system model in order to apply digital signal processing techniques
for asynchronous multi-user detection. The goal is to develop a
finite observation interval for the received vector 
which
can be modeled in discrete time.
The sampling at the receiver will be at the chip rate, and the
observation interval will be of length 2T. In the asynchronous model, it
is necessary for the observation interval to be at least 2T in order to
guarantee that one complete bit from the desired user will fall in the
interval. For simplicity, we will define the continuous time chip
waveform 
as a
rectangular pulse of period 
, and amplitude 1. This is not a
practical choice for a pulse shaping filter, but the following
derivations can be extended to the raised-cosine pulse shape. In the
case of non-rectangular pulse shapes, overlapping chips and bits will cause
integrals to appear in the expressions for 
, the sampled
received vector.
Proceeding with the rectangular pulse shaping assumption,
the discrete time received sample is
.
, the kth user's contribution, where
If we assume that we are synchronized at the chip rate, but we are not
synchronized with any one user at the bit rate, then each user's received
vector , will have contributions from 
, 
, and
where is the bit of user k at time n.
Let 
be a length 2L vector contain the spreading sequence
for user k and L zeros.
Also, let 
denote the acyclic left shift operator, and 
be the right acyclic shift operator operating on vectors of length 2N.
For example, for a vector 
,
and
. Let 
denote the integer chip delay from the left hand side of the observation
interval to the first chip of user k's nth bit. Now, for the
contribution to the received signal from user k at observation
interval n, we have
Where
So the resulting received vector for user k is a linear combination
of three vectors each modulating a differed bit. An example
demonstrating this technique follows in the next section.
Ideally we would like to relate this asynchronous development to our
original matrices in the bit synchronous case. When we are demodulating
user k's signal, we must have timing acquisition for user k. If
we assume we have timing synchronization, then we only have to
redefine our 
matrix 
as
