Generation of Received Data

To generate realistic data with certain desired characteristics, many variables have to be chosen. Using a variation of the system model developed in chapter 2, many of these variables were easily incorporated in the generation of the received data, including user power, pulse shaping, asynchronism, delay, and spreading codes. In order to make a reasonably sized GUI, many of these parameters are chosen randomly. However, the distribution of these parameters can be manipulated through the GUI. For example, to make a realistic system, each user must have a different channel. Instead of defining each channel tap by tap, we can generate the channels randomly by specifying the distribution of the multipath. The drawback is that this limits the user's control over the individual channels. In order to make up for this limitation, there is an option for defining a specific user's power compared to all the others. For instance, you can make one user 10 dB stronger than all the others. Since the purpose of this software is to compare the general performance of linear detectors given certain system parameters, the control of individual user's parameters is limited. This design choice was made to make the GUI more usable and more readily extendable to Monte Carlo simulations. The user delay, power, noise, and spreading codes are also generated randomly. More details will follow in section 4.3.

In developing the software for generating the received data, a large portion of time was spent computing the final data. Generating data using the asynchronous model developed in chapter 2 turns out to be extremely inefficient. Since the pulse shaping filter is not a brick wall filter assumed in the derivations, the equation for the spreading matrix is no longer,

Also, even if we recalculate the spreading matrix for the square root raised cosine pulse shaping filter, using is not an efficient technique for generating the data. If , then the regressor for each symbol iteration contains overlapping data. You can see this for 2 iterations when , L=4, and .
Iteration 1 l=0

Iteration 2 l=L

As you can see, every iteration will recalculate three chip spaced information bits which were calculated in the previous iteration. When , this approach will not work at all, because there will be missing chip information between iterations. A different method was used to generate the received data.

In order to incorporate asynchronism and delay into the received data, we changed the channel model to include these parameters. To implement this, a square root raised cosine pulse, oversampled at 32 times the chip-rate, was created. Then a vector containing the number of multipath rays specified, also sampled at 32 times the chip rate, was generated. The two of these were convolved and sampled at a rate equal to . The initial sampling position was chosen using two parameters. The first requiring that the largest channel tap be in the middle given , and the second adjusting for individual chip asynchronism by adding a fraction of 32 to the initial sampling position. Bit asynchronism was implemented by simply zero padding the resulting channel taps. Figure 4.4 shows the pulse shape, oversampled multipath vector, and the sampled convolution. To see the final channel impulse response see figure 4.6. Notice there are only non-zero channel taps, and the rest are zero. These zero taps represent the bit asynchronous delay.

To actually generate the received data vector, the structure of was exploited. It can be shown, [9] that has the form

where,

and are the components of the users channel and spreading sequence respectively. It is useful to show the multi-rate block diagram in figure 4.1 to see how we can use this fact to our advantage when creating the received data, .

  
Figure 4.1: Multi-Rate DS-CDMA model employed to generate received data

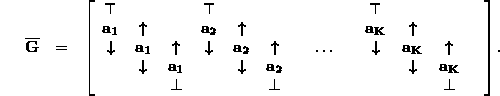
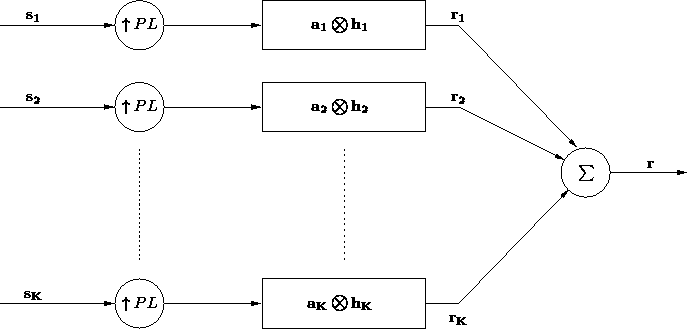
We can generate each by convolving with the upsampled version of . This convolution is computationally inexpensive because many of the terms in the convolution are zero, allowing a polyphase implementation of the impulse response defined by . Finally, is generated simply by,