3.2 Two-tap equalizer with six-tap undermodeled channel and BPSK source

Again consider the communications system in Figure 1 with an i.i.d. BPSK source, the (undermodeled) channel given by $\ensuremath{\mathbf{c}}=\left[\begin{array} {cccccc}0.1&0.3&1&-0.1&0.5&0.2\end{array}\right]^T$, and a two-tap FSE (N_f=2).

  

Figure 4: SE-CMA cost contours for undermodeled case with BPSK source, 15 dB SNR

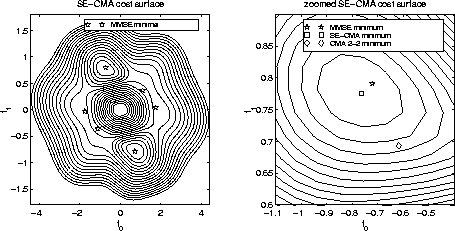Figure 4 shows the SE-CMA cost contours for this system when the SNR is 15 dB. Once again, the SE-CMA minimum is closer to the MMSE minimum than is CMA 2-2.

For 40,000 iterations with 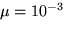$\mu=10^{-3}$, a portion of the squared-error history for a simulation is shown in Figure 5 for a system with an SNR of 15 dB.

  

Figure 5: Comparison of error history for SE-CMA and CMA 2-2 (BPSK, 6-tap undermodeled channel)

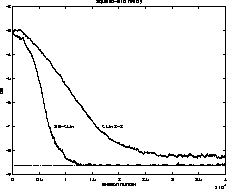As shown, SE-CMA attains a lower error than CMA 2-2 in this undermodeled example as well.