1.2.2 SE-CMA (for real-valued source)

To improve computational efficiency, a signed-error algorithm modifies the equalizer update equation of the unsigned algorithm by retaining only the sign of the error function, thereby eliminating a multiply operation. This brings about SE-CMA which has the following equalizer update equation [1]:

It has been shown that SE-CMA is equivalent to CMA 1-1 where p,q=1 in (1). Consider the CMA 1-1 cost function $J_{cma_{1,1}} = E\bigl\{ \bigl\vert \vert y_n\vert-\beta \bigr\vert \bigr\}$ and corresponding update equation $\ensuremath{\mathbf{f}}(n+1) = \ensuremath{\mathbf{f}}(n)+ \mu \ensuremath{\mathbf{r}}(n)\sgn(y_n(\beta-\vert y_n\vert))$. This CMA 1-1 update equation is identical to the SE-CMA update equation when $\beta=\sqrt{\gamma}$. Thus,

Selection of $\gamma$ for which SE-CMA converges to the perfect equalizer in the noiseless case is performed as follows. The dispersion constant $\gamma$ should be chosen such that $\gamma=a_\nu^2$ where $a_\nu$ is the $\nu^{th}$ positive member of the source alphabet and integer $\nu$ satisfies

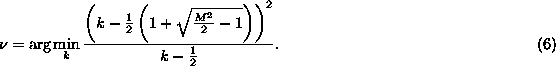
For some of the common real-valued alphabets of unit source variance, (6) suggests the following choice for $\gamma$:

 

$$\gamma$$ Alphabet

BPSK 1

4-PAM 9/5

8-PAM 25/21

16-PAM 121/85

32-PAM 529/341

In the presence of noise, a recent paper [2] has suggested that $\gamma$ should be chosen based on the expected SNR. See section 4 for further discussion.