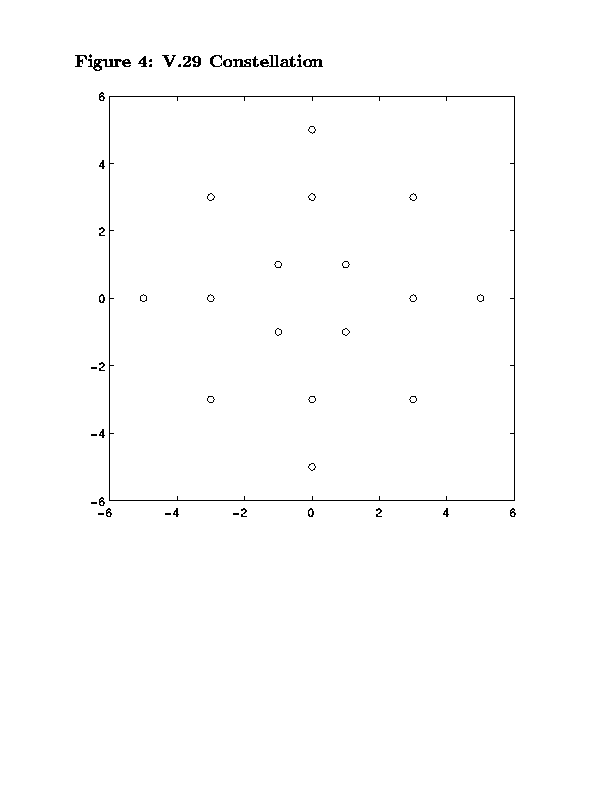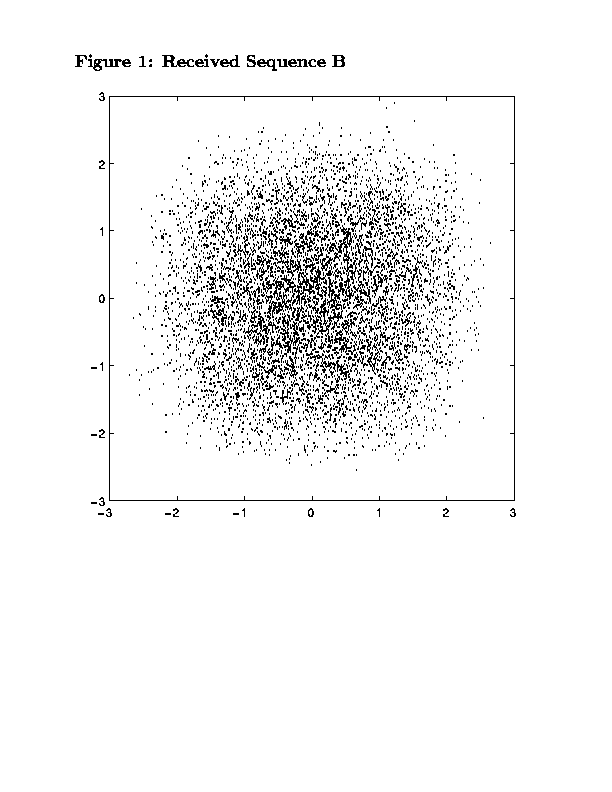
We begin by taking the 2nd random sequence used provided in the Modem Data section and then plotting the received signal set in the complex plane (see Figure 1). Notice that the eye is closed. The sequence contains about 23,000 T/2-spaced samples, not enough data for CMA to open the eye with the stepsize of 0.00001 used. Thus, the data sequence is repeated 6 times to a length of about 138,000 T/2-spaced samples.
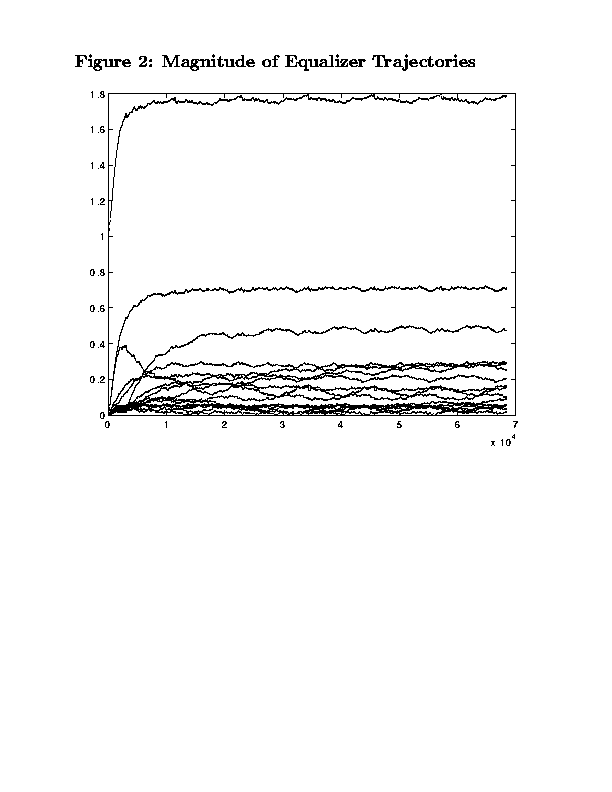
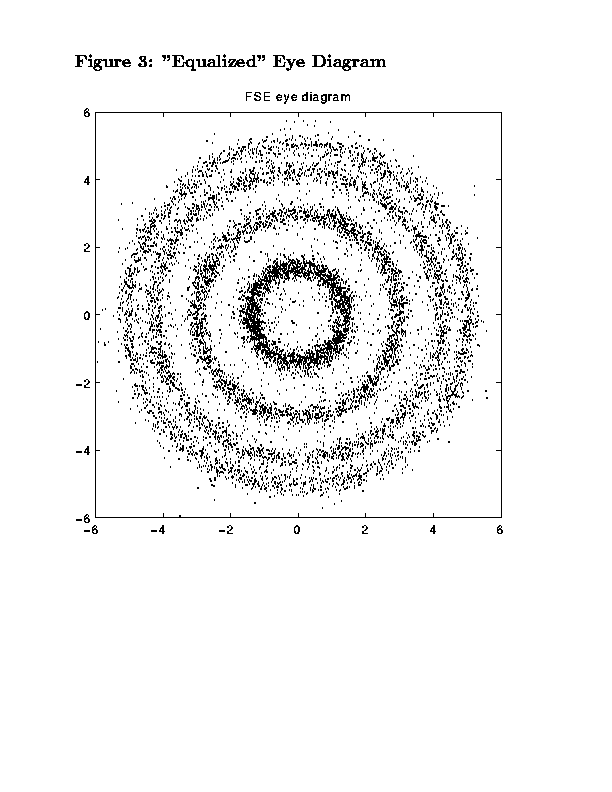
The magnitude of the parameter trajectories at each on-baud sample from a center spike initialization for a 16-tap FSE are shown in Figure 2. The eye diagram for the whole data record with the adaptive equalizer fixed at its value on the last iteration is shown in Figure 3. Notice that the algorithm does not distinguish distinct constellation points, such as shown in the tutorial CMA on Microwave Channel. Rather, concentric rings of different moduli are formed. The reason for this rotating version of a V.29 constellation is the small error in carrier frequency/phase lock at the receiver. CMA is still successful in its convergence to an eye-opening FSE parameterization due to the CMA cost function's invariance to carrier phase. Typically, this problem is overcome by adding a phase-locked loop after FSE-CMA to acquire the carrier phase. One would then expect to observe clusters around the 16 V.29 constellation points, shown in Figure 4. Compare the four rings that would result with rotation of Figure 4 to the "equalized" spinning constellation in Figure 3.
Matlab code to simulate adaptive blind equalization using CMA is available in fsecma.m.